2008年四川省高考数学试卷(文科)(含解析版)
2008年四川省高考数学试卷(文科)
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)已知全集U={1,2,3,4,5},集合A={1,3},B={3,4,5},则集合∁U(A∩B)=( )
A.{3}B.{4,5} C.{3,4,5} D.{1,2,4,5}
2.(5分)函数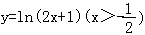 的反函数是( )
的反函数是( )
A.![]() B.y=e2x﹣1(x∈R)
B.y=e2x﹣1(x∈R)
C.![]() D.
D.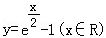
3.(5分)设平面向量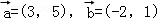 ,则
,则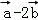 =( )
=( )
A.(7,3)B.(7,7) C.(1,7) D.(1,3)
4.(5分)(tanx+cotx)cos2x=( )
A.tanxB.sinx C.cosx D.cotx
5.(5分)不等式|x2﹣x|<2的解集为( )
A.(﹣1,2)B.(﹣1,1) C.(﹣2,1) D.(﹣2,2)
6.(5分)直线y=3x绕原点逆时针旋转90°,再向右平移1个单位,所得到的直线为( )
A.![]() B.
B.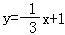 C.y=3x﹣3 D.
C.y=3x﹣3 D.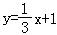
7.(5分)△ABC的三内角A、B、C的对边边长分别为a、b、c.若a=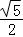 b,A=2B,则cos B=( )
b,A=2B,则cos B=( )
A.![]() B.
B.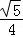 C.
C.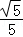 D.
D.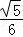
8.(5分)设M是球心O的半径OP的中点,分别过M,O作垂直于OP的平面,截球面得两个圆,则这两个圆的面积比值为:( )
A.![]() B.
B.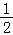 C.
C.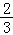 D.
D.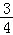
9.(5分)设定义在R上的函数f(x)满足f(x)•f(x+2)=13,若f(1)=2,则f(99)=( )
A.13B.2 C.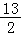 D.
D.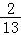
10.(5分)设直线l⊂平面α,过平面α外一点A与l,α都成30°角的直线有且只有( )
A.1条B.2条 C.3条 D.4条
11.(5分)已知双曲线C: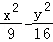 =1的左右焦点分别为F1,F2,P为C的右支上一点,且|PF2|=|F1F2|,则△PF1F2的面积等于( )
=1的左右焦点分别为F1,F2,P为C的右支上一点,且|PF2|=|F1F2|,则△PF1F2的面积等于( )
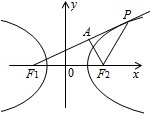
A.24B.36 C.48 D.96
12.(5分)若三棱柱的一个侧面是边长为2的正方形,另外两个侧面都是有一个内角为60°的菱形,则该棱柱的体积等于( )
A.![]() B.
B.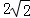 C.
C.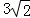 D.
D.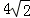
二、填空题(共4小题,每小题4分,满分16分)
13.(4分)(1+2x)3(1﹣x)4展开式中x2的系数为 .
14.(4分)已知直线l:x﹣y+4=0与圆C:(x﹣1)2+(y﹣1)2=2,则C上各点到l的距离的最小值为 .
15.(4分)从甲、乙等10名同学中挑选4名参加某校公益活动,要求甲、乙中至少有1人参加,则不同的挑选方法共有 种.
16.(4分)设数列{an}中,a1=2,an+1=an+n+1,则通项an= .
三、解答题(共6小题,满分74分)
17.(12分)求函数y=7﹣4sinxcosx+4cos2x﹣4cos4x的最大值与最小值.
18.(12分)设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的3位顾客中至少有2位顾客既未购买甲种也未购买乙种商品的概率.
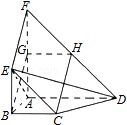
19.(12分)如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC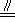
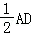 ,BE
,BE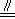
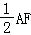 ,G,H分别为FA,FD的中点
,G,H分别为FA,FD的中点
(Ⅰ)证明:四边形BCHG是平行四边形;
(Ⅱ)C,D,F,E四点是否共面?为什么?
(Ⅲ)设AB=BE,证明:平面ADE⊥平面CDE.
20.(12分)设x=1和x=2是函数f(x)=x5+ax3+bx+1的两个极值点.
(Ⅰ)求a和b的值;
(Ⅱ)求f(x)的单调区间.
21.(12分)设数列{an}的前n项和为Sn=2an﹣2n,
(Ⅰ)求a1,a4
(Ⅱ)证明:{an+1﹣2an}是等比数列;
(Ⅲ)求{an}的通项公式.
22.(14分)设椭圆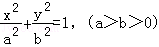 的左右焦点分别为F1,F2,离心率
的左右焦点分别为F1,F2,离心率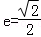 ,点F2到右准线为l的距离为
,点F2到右准线为l的距离为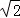
(Ⅰ)求a,b的值;
(Ⅱ)设M,N是l上的两个动点,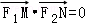 ,
,
证明:当|MN|取最小值时,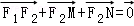 .
.
2008年四川省高考数学试卷(文科)
参考答案与试题解析
一、选择题(共12小题,每小题5分,满分60分)
1.(5分)已知全集U={1,2,3,4,5},集合A={1,3},B={3,4,5},则集合∁U(A∩B)=( )
A.{3} B.{4,5} C.{3,4,5} D.{1,2,4,5}
【考点】1H:交、并、补集的混合运算.菁优网版权所有
【分析】根据交集的含义求A∩B、再根据补集的含义求解.
【解答】解:A={1,3},B={3,4,5}⇒A∩B={3};
所以CU(A∩B)={1,2,4,5},
故选:D.
【点评】本题考查集合的基本运算,较简单.
2.(5分)函数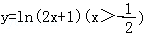 的反函数是( )
的反函数是( )
A.![]() B.y=e2x﹣1(x∈R)
B.y=e2x﹣1(x∈R)
C.![]() D.
D.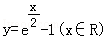
【考点】4G:指数式与对数式的互化;4R:反函数.菁优网版权所有
【分析】反解得解析式,或利用原函数与反函数的定义域与值域的互换对选项进行淘汰
【解答】解:∵由y=ln(2x+1)反解得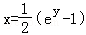 ∴
∴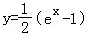 从而淘汰B、D、
从而淘汰B、D、
又∵原函数定义域为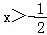 ∴反函数值域为
∴反函数值域为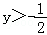
故选:C.
【点评】此题重点考查求反函数的方法,考查原函数与反函数的定义域与值域的互换性
3.(5分)设平面向量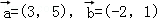 ,则
,则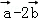 =( )
=( )
A.(7,3)B.(7,7) C.(1,7) D.(1,3)
【考点】9J:平面向量的坐标运算.菁优网版权所有
【分析】根据向量的坐标运算法则即可解题.
【解答】解:∵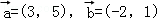 ∴
∴
故选:A.
【点评】此题重点考查向量加减、数乘的坐标运算;应用向量的坐标运算公式是解题的关键;
4.(5分)(tanx+cotx)cos2x=( )
A.tanxB.sinx C.cosx D.cotx
【考点】GG:同角三角函数间的基本关系.菁优网版权所有
【分析】此题重点考查各三角函数的关系,切化弦,约分整理,凑出同一角的正弦和余弦的平方和,再约分化简.
【解答】解:∵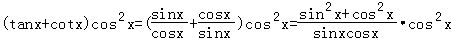 =
=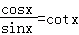
故选:D.
【点评】将不同的角化为同角;将不同名的函数化为同名函数,以减少函数的种类;当式中有正切、余切、正割、余割时,通常把式子化成含有正弦与余弦的式子,即所谓“切割化弦”.
5.(5分)不等式|x2﹣x|<2的解集为( )
A.(﹣1,2)B.(﹣1,1) C.(﹣2,1) D.(﹣2,2)
【考点】7E:其他不等式的解法.菁优网版权所有
【分析】可由绝对值的意义去绝对值,可用公式法,平方法,特值验证淘汰法
【解答】解:∵|x2﹣x|<2∴﹣2<x2﹣x<2即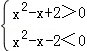 ,
,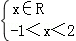 ,∴x∈(﹣1,2)
,∴x∈(﹣1,2)
故选:A.
【点评】此题重点考查绝对值不等式和二次不等式的解法,属基本题.准确进行不等式的转化去掉绝对值符号为解题的关键
6.(5分)直线y=3x绕原点逆时针旋转90°,再向右平移1个单位,所得到的直线为( )
A.![]() B.
B.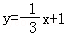 C.y=3x﹣3 D.
C.y=3x﹣3 D.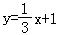
【考点】IA:两条直线垂直与倾斜角、斜率的关系.菁优网版权所有
【分析】先利用两直线垂直写出第一次方程,再由平移写出第二次方程.
【解答】解:∵直线y=3x绕原点逆时针旋转90°
∴两直线互相垂直
则该直线为 ,
,
那么将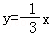 向右平移1个单位得
向右平移1个单位得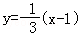 ,即
,即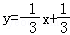
故选:A.
【点评】本题主要考查互相垂直的直线关系,同时考查直线平移问题.
7.(5分)△ABC的三内角A、B、C的对边边长分别为a、b、c.若a=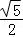 b,A=2B,则cos B=( )
b,A=2B,则cos B=( )
A.![]() B.
B. C.
C.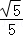 D.
D.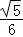
【考点】HP:正弦定理.菁优网版权所有
【专题】11:计算题.
【分析】通过正弦定理得出sinA和sinB的方程组,求出cosB的值.
【解答】解:∵△ABC中,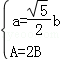 ,
,
∴根据正弦定理得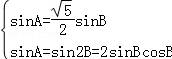
∴
故选:B.
【点评】本题主要考查了正弦定理的应用.在解三角形中,利用正余弦定理进行边角转化是解题的基本方法,在三角函数的化简求值中常要重视角的统一,函数的统一,降次思想的应用.
8.(5分)设M是球心O的半径OP的中点,分别过M,O作垂直于OP的平面,截球面得两个圆,则这两个圆的面积比值为:( )
A.![]() B.
B.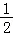 C.
C.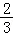 D.
D.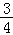
【考点】L*:球面距离及相关计算.菁优网版权所有
【分析】可通过数形结合的方法,画出图形,再利用勾股定理进行求解.
【解答】解:设分别过M,O作垂线于OP的面截球得三个圆的半径为r1,r2,球半径为R,
则:
∴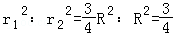
∴这两个圆的面积比值为: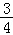
故选:D.
【点评】此题重点考查球中截面圆半径,球半径之间的关系.
9.(5分)设定义在R上的函数f(x)满足f(x)•f(x+2)=13,若f(1)=2,则f(99)=( )
A.13B.2 C.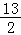 D.
D.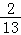
【考点】3T:函数的值.菁优网版权所有
【专题】16:压轴题.
【分析】根据f(1)=2,f(x)•f(x+2)=13先求出f(3)=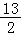 ,再由f(3)求出f(5),依次求出f(7)、f(9)观察规律可求出f(x)的解析式,最终得到答案.
,再由f(3)求出f(5),依次求出f(7)、f(9)观察规律可求出f(x)的解析式,最终得到答案.
【解答】解:∵f(x)•f(x+2)=13且f(1)=2
∴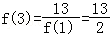 ,
,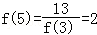 ,
,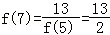 ,
,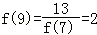 ,
,
∴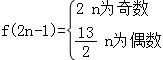 ,
,
∴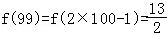
故选:C.
【点评】此题重点考查递推关系下的函数求值;此类题的解决方法一般是求出函数解析式后代值,或者得到函数的周期性求解.
10.(5分)设直线l⊂平面α,过平面α外一点A与l,α都成30°角的直线有且只有( )
A.1条B.2条 C.3条 D.4条
【考点】LP:空间中直线与平面之间的位置关系.菁优网版权所有
【分析】利用圆锥的母线与底面所成的交角不变画图,即可得到结果.
【解答】解:如图,和α成30°角的直线一定是以A为顶点的圆锥的母线所在直线,当∠ABC=∠ACB=30°,直线AC,AB都满足条件
故选:B.
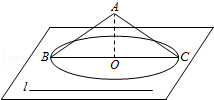
【点评】此题重点考查线线角,线面角的关系,以及空间想象能力,图形的对称性;
数形结合,重视空间想象能力和图形的对称性;
11.(5分)已知双曲线C: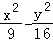 =1的左右焦点分别为F1,F2,P为C的右支上一点,且|PF2|=|F1F2|,则△PF1F2的面积等于( )
=1的左右焦点分别为F1,F2,P为C的右支上一点,且|PF2|=|F1F2|,则△PF1F2的面积等于( )
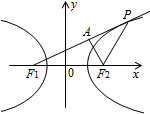
A.24B.36 C.48 D.96
【考点】KC:双曲线的性质.菁优网版权所有
【专题】11:计算题;16:压轴题.
【分析】先根据双曲线方程求出焦点坐标,再利用双曲线的第一定义求得||PF1|,作PF1边上的高AF2则可知AF1的长度,进而利用勾股定理求得AF2,则△PF1F2的面积可得.
【解答】解:∵双曲线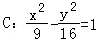 中a=3,b=4,c=5,
中a=3,b=4,c=5,
∴F1(﹣5,0),F2(5,0)
∵|PF2|=|F1F2|,
∴|PF1|=2a+|PF2|=6+10=16
作PF1边上的高AF2,则AF1=8,
∴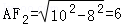
∴△PF1F2的面积为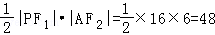
故选:C.
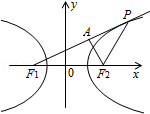
【点评】此题重点考查双曲线的第一定义,双曲线中与焦点,准线有关三角形问题;由题意准确画出图象,利用数形结合,注意到三角形的特殊性.
12.(5分)若三棱柱的一个侧面是边长为2的正方形,另外两个侧面都是有一个内角为60°的菱形,则该棱柱的体积等于( )
A.![]() B.
B.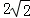 C.
C.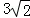 D.
D.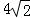
【考点】LF:棱柱、棱锥、棱台的体积.菁优网版权所有
【专题】11:计算题;16:压轴题.
【分析】先求侧棱与底面所成角的余弦,然后求出棱柱的高,再求棱柱的体积.
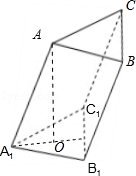
【解答】解:如图在三棱柱ABC﹣A1B1C1中,设∠AA1B1=∠AA1C1=60°,
由条件有∠C1A1B1=60°,作AO⊥面A1B1C1于点O,
则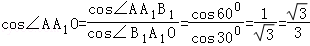
∴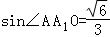 ∴
∴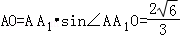
∴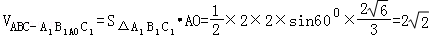
故选:B.
【点评】此题重点考查立体几何中的最小角定理和柱体体积公式,同时考查空间想象能力;具有较强的空间想象能力,准确地画出图形是解决此题的前提,熟悉最小角定理并能准确应用是解决此题的关键.
二、填空题(共4小题,每小题4分,满分16分)
13.(4分)(1+2x)3(1﹣x)4展开式中x2的系数为 ﹣6 .
【考点】DA:二项式定理.菁优网版权所有
【专题】11:计算题.
【分析】利用乘法原理找展开式中的含x2项的系数,注意两个展开式的结合分析,即分别为第一个展开式的常数项和第二个展开式的x2的乘积、第一个展开式的含x项和第二个展开式的x项的乘积、第一个展开式的x2的项和第二个展开式的常数项的乘积之和从而求出答案.
【解答】解:∵(1+2x)3(1﹣x)4展开式中x2项为
C3013(2x)0•C4212(﹣x)2+C3112(2x)1•C4113(﹣x)1+C3212(2x)2•C4014(﹣x)0
∴所求系数为C30•C42+C31•2•C41(﹣1)+C32•22•C4014=6﹣24+12=﹣6.
故答案为:﹣6.
【点评】此题重点考查二项展开式中指定项的系数,以及组合思想,重在找寻这些项的来源.
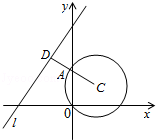
14.(4分)已知直线l:x﹣y+4=0与圆C:(x﹣1)2+(y﹣1)2=2,则C上各点到l的距离的最小值为 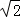 .
.
【考点】IT:点到直线的距离公式;J9:直线与圆的位置关系.菁优网版权所有
【专题】31:数形结合.
【分析】如图过点C作出CD与直线l垂直,垂足为D,与圆C交于点A,则AD为所求;求AD的方法是:由圆的方程找出圆心坐标与圆的半径,然后利用点到直线的距离公式求出圆心到直线l的距离d,利用d减去圆的半径r即为圆上的点到直线l的距离的最小值.
【解答】解:如图可知:过圆心作直线l:x﹣y+4=0的垂线,则AD长即为所求;
∵圆C:(x﹣1)2+(y﹣1)2=2的圆心为C(1,1),半径为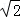 ,
,
点C到直线l:x﹣y+4=0的距离为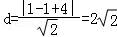 ,
,
∴AD=CD﹣AC=2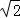 ﹣
﹣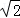 =
=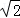 ,
,
故C上各点到l的距离的最小值为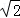 .
.
故答案为: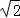
【点评】此题重点考查圆的标准方程和点到直线的距离.本题的突破点是数形结合,使用点C到直线l的距离距离公式.
15.(4分)从甲、乙等10名同学中挑选4名参加某校公益活动,要求甲、乙中至少有1人参加,则不同的挑选方法共有 140 种.
【考点】D5:组合及组合数公式.菁优网版权所有
【专题】11:计算题;16:压轴题.
【分析】要求甲、乙中至少有1人参加的对立事件是甲和乙都不参加,所以从事件的反面入手来解,从10个同学中挑选4名参加某项公益活动的结果数减去从甲、乙之外的8个同学中挑选4名参加某项公益活动的结果数.
【解答】解:∵从10个同学中挑选4名参加某项公益活动有C104种不同挑选方法,
从甲、乙之外的8个同学中挑选4名参加某项公益活动有C84种不同挑选方法;
∴甲、乙中至少有1人参加,则不同的挑选方法共有C104﹣C84=210﹣70=140种不同挑选方法
故答案为:140.
【点评】此题重点考查组合的意义和组合数公式,由题目中的“至少”知道从反面排除易于解决,这和概率中的对立事件考虑方法一样,正难则反原则.
16.(4分)设数列{an}中,a1=2,an+1=an+n+1,则通项an= 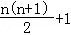 .
.
【考点】8H:数列递推式.菁优网版权所有
【专题】11:计算题;16:压轴题.
【分析】根据数列的递推式,依次写出n=1,2,3…n的数列相邻两项的关系,进而各式相加即可求得答案.
【解答】解:∵a1=2,an+1=an+n+1
∴an=an﹣1+(n﹣1)+1,an﹣1=an﹣2+(n﹣2)+1,an﹣2=an﹣3+(n﹣3)+1,…,a3=a2+2+1,a2=a1+1+1,a1=2=1+1
将以上各式相加得:an=[(n﹣1)+(n﹣2)+(n﹣3)+…+2+1]+n+1
=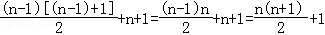
故答案为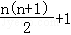 ;
;
【点评】此题重点考查由数列的递推公式求数列的通项公式.重视递推公式的特征与解法的选择;抓住an+1=an+n+1中an+1,an系数相同是找到方法的突破口;此题可用累和法,迭代法等;
三、解答题(共6小题,满分74分)
17.(12分)求函数y=7﹣4sinxcosx+4cos2x﹣4cos4x的最大值与最小值.
【考点】HW:三角函数的最值.菁优网版权所有
【专题】11:计算题.
【分析】利用二倍角的正弦函数公式及同角三角函数间的基本关系化简y的解析式后,再利用配方法把y变为完全平方式即y=(1﹣sin2x)2+6,可设z═(u﹣1)2+6,u=sin2x,因为sin2x的范围为[﹣1,1],根据u属于[﹣1,1]时,二次函数为递减函数,利用二次函数求最值的方法求出z的最值即可得到y的最大和最小值.
【解答】解:y=7﹣4sinxcosx+4cos2x﹣4cos4x=7﹣2sin2x+4cos2x(1﹣cos2x)=7﹣2sin2x+4cos2xsin2x=7﹣2sin2x+sin22x=(1﹣sin2x)2+6
由于函数z=(u﹣1)2+6在[﹣1,1]中的最大值为zmax=(﹣1﹣1)2+6=10
最小值为zmin=(1﹣1)2+6=6
故当sin2x=﹣1时y取得最大值10,当sin2x=1时y取得最小值6
【点评】此题重点考查三角函数基本公式的变形,配方法,符合函数的值域及最值;本题的突破点是利用倍角公式降幂,利用配方变为复合函数,重视复合函数中间变量的范围是关键.
18.(12分)设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6,且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(Ⅰ)求进入商场的1位顾客购买甲、乙两种商品中的一种的概率;
(Ⅱ)求进入商场的3位顾客中至少有2位顾客既未购买甲种也未购买乙种商品的概率.
【考点】C8:相互独立事件和相互独立事件的概率乘法公式.菁优网版权所有
【专题】11:计算题.
【分析】(1)由题意知购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.设出事件,知事件之间是相互独立的和互斥的,根据概率公式得到结果.
(2)进入商场的3位顾客中至少有2位顾客既未选购甲种商品,也未选选购乙种商品包括进入商场的3位顾客中都未选购甲种商品,也未选购买乙种商品和进入商场的2位顾客未选购甲种商品,也未选购买乙种商品.根据事件之间的关系,得到结果.
【解答】解:(Ⅰ)由题意知购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
记A表示事件:进入商场的1位顾客购买甲种商品,
记B表示事件:进入商场的1位顾客购买乙种商品,
记C表示事件:进入商场的1位顾客购买甲、乙两种商品中的一种,
A与B 是相互独立的,且A 与
与 B是互斥的,
B是互斥的,
∵C=A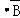 +
+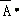 B
B
∴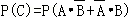
=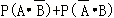 =
=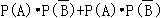
=0.5×0.4+0.5×0.6=0.5
(Ⅱ)记A2表示事件:进入商场的3位顾客中都未选购甲种商品,也未选购买乙种商品;
D表示事件:进入商场的1位顾客未选购甲种商品,也未选购买乙种商品;
E表示事件:进入商场的3位顾客中至少有2位顾客既未选购甲种商品,也未选选购乙种商品;
∵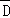 =
= ,
,
∴P(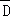 )=P(
)=P(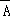 )•P(
)•P(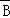 )
)
=0.5×0.4=0.2
P(A1)=C32×0.22×0.8=0.096
P(A2)=0.23=0.008
P(E)=P(A1+A2)=P(A1)+P(A2)=0.096+0.008=0.104
【点评】此题重点考查相互独立事件有一个发生的概率,分清相互独立事件的概率求法,对于“至少”常从反面入手常可起到简化的作用;
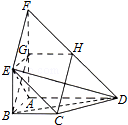
19.(12分)如图,平面ABEF⊥平面ABCD,四边形ABEF与ABCD都是直角梯形,∠BAD=∠FAB=90°,BC
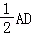 ,BE
,BE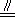
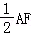 ,G,H分别为FA,FD的中点
,G,H分别为FA,FD的中点
(Ⅰ)证明:四边形BCHG是平行四边形;
(Ⅱ)C,D,F,E四点是否共面?为什么?
(Ⅲ)设AB=BE,证明:平面ADE⊥平面CDE.
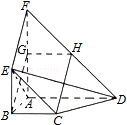
【考点】LO:空间中直线与直线之间的位置关系;LY:平面与平面垂直;MN:向量语言表述面面的垂直、平行关系.菁优网版权所有
【专题】15:综合题;35:转化思想.
【分析】解法1:(Ⅰ)直接证明GH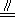 BC推出四边形BCHG是平行四边形.
BC推出四边形BCHG是平行四边形.
(Ⅱ)C,D,F,E四点共面.推出EF∥CH,就是EC,FH共面.又点D在直线FH上所以C,D,F,E四点共面.
(Ⅲ)连接EC,证明BG⊥EA.BG⊥ED,ED∩EA=E,推出BG⊥平面ADE,然后证明平面ADE⊥平面CDE.
解法2:由平面ABEF⊥平面ABCD,AF⊥AB,得AF⊥平面ABCD,以A为坐标原点,射线AB为x轴正半轴,建立如图所示的直角坐标系A﹣xyz
(Ⅰ)通过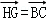 ,又点G不在直线BC上,说明四边形BCHG是平行四边形.
,又点G不在直线BC上,说明四边形BCHG是平行四边形.
(Ⅱ)C,D,F,E四点共面.利用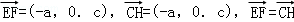 ,又C∉EF,H∈FD,证明C,D,E,F四点共面.
,又C∉EF,H∈FD,证明C,D,E,F四点共面.
(Ⅲ)通过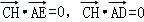 ,即CH⊥AE,CH⊥AD,说明平面ADE⊥平面CDE
,即CH⊥AE,CH⊥AD,说明平面ADE⊥平面CDE
【解答】解法1:(Ⅰ)由题意知,FG=GA,FH=HD
所以GH
又BC
 ,故GH
,故GH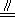 BC
BC
所以四边形BCHG是平行四边形.
(Ⅱ)C,D,F,E四点共面.理由如下:
由BE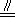
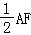 ,G是FA的中点知,BE
,G是FA的中点知,BE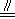 GF,所以EF∥BG
GF,所以EF∥BG
由(Ⅰ)知BG∥CH,所以EF∥CH,故EC,FH共面.又点D在直线FH上
所以C,D,F,E四点共面.
(Ⅲ)连接EG,由AB=BE,BE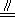 AG及∠BAG=90°知ABEG是正方形
AG及∠BAG=90°知ABEG是正方形
故BG⊥EA.由题设知FA,AD,AB两两垂直,故AD⊥平面FABE,
因此EA是ED在平面FABE内的射影,根据三垂线定理,BG⊥ED
又ED∩EA=E,所以BG⊥平面ADE
由(Ⅰ)知CH∥BG,所以CH⊥平面ADE.
由(Ⅱ)知F∈平面CDE,故CH⊂平面CDE,得平面ADE⊥平面CDE
解法2:由平面ABEF⊥平面ABCD,AF⊥AB,得AF⊥平面ABCD,
以A为坐标原点,射线AB为x轴正半轴,建立如图所示的直角坐标系A﹣xyz
(Ⅰ)设AB=a,BC=b,BE=c,则由题设得A(0,0,0),B(a,0,0),C(a,b,0),D(0,2b,0),E(a,0,c),G(0,0,c),H(0,b,c)
所以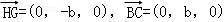
于是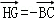
又点G不在直线BC上
所以四边形BCHG是平行四边形.
(Ⅱ)C,D,F,E四点共面.理由如下:
由题设知F(0,0,2c),所以
又C∉EF,H∈FD,故C,D,E,F四点共面.
(Ⅲ)由AB=BE得,所以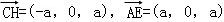
又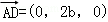 ,因此
,因此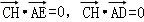
即CH⊥AE,CH⊥AD
又AD∩AE=A,所以CH⊥平面ADE
故由CH⊂平面CDFE,得平面ADE⊥平面CDE

【点评】此题重点考查立体几何中直线与直线的位置关系,四点共面问题,面面垂直问题,考查了空间想象能力,几何逻辑推理能力,以及计算能力;熟悉几何公理化体系,准确推理,注意逻辑性是顺利进行解法1的关键;在解法2中,准确的建系,确定点坐标,熟悉向量的坐标表示,熟悉空间向量的计算在几何位置的证明,在有关线段,角的计算中的计算方法是解题的关键.
20.(12分)设x=1和x=2是函数f(x)=x5+ax3+bx+1的两个极值点.
(Ⅰ)求a和b的值;
(Ⅱ)求f(x)的单调区间.
【考点】6B:利用导数研究函数的单调性;6C:函数在某点取得极值的条件.菁优网版权所有
【专题】11:计算题.
【分析】(I)利用函数的导数在极值点处的值为0,列出方程组,求出a,b的值.
(Ⅱ)将a,b的值代入导函数,令导函数大于0求出解集为递增区间;令导函数小于0,求出解集为递减区间.
【解答】解:(Ⅰ)因为f′(x)=5x4+3ax2+b
由假设知:f′(1)=5+3a+b=0,f′(2)=24×5+22×3a+b=0
解得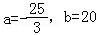
(Ⅱ)由(Ⅰ)知f′(x)=5x4+3ax2+b=5(x2﹣1)(x2﹣4)=5(x+1)(x+2)(x﹣1)(x﹣2)
当x∈(﹣∞,﹣2)∪(﹣1,1)∪(2,+∞)时,f′(x)>0
当x∈(﹣2,﹣1)∪(1,2)时,f′(x)<0
因此f(x)的单调增区间是(﹣∞,﹣2),(﹣1,1),(2,+∞)
f(x)的单调减区间是(﹣2,﹣1),(1,2)
【点评】本题考查函数的极值点处的导数值为0、考查函数的单调性与导函数的符号有关:导函数大于0时,函数递增;导函数小于0时,函数递减.
21.(12分)设数列{an}的前n项和为Sn=2an﹣2n,
(Ⅰ)求a1,a4
(Ⅱ)证明:{an+1﹣2an}是等比数列;
(Ⅲ)求{an}的通项公式.
【考点】87:等比数列的性质;88:等比数列的通项公式;8H:数列递推式.菁优网版权所有
【专题】11:计算题;14:证明题;16:压轴题.
【分析】(Ⅰ)令n=1得到s1=a1=2并推出an,令n=2求出a2,s2得到a3推出a4即可;
(Ⅱ)由已知得an+1﹣2an=(Sn+2n+1)﹣(Sn+2n)=2n+1﹣2n=2n即为等比数列;
(Ⅲ)an=(an﹣2an﹣1)+2(an﹣1﹣2an﹣2)+…+2n﹣2(a2﹣2a1)+2n﹣1a1=(n+1)•2n﹣1即可.
【解答】解:(Ⅰ)因为a1=S1,2a1=S1+2,所以a1=2,S1=2,
由2an=Sn+2n知:2an+1=Sn+1+2n+1=an+1+Sn+2n+1,
得an+1=sn+2n+1①,
则a2=S1+22=2+22=6,S2=8;a3=S2+23=8+23=16,S2=24,a4=S3+24=40;
(Ⅱ)由题设和①式知an+1﹣2an=(Sn+2n+1)﹣(Sn+2n)=2n+1﹣2n=2n
所以{an+1﹣2an}是首项为2,公比为2的等比数列.
(Ⅲ)an=(an﹣2an﹣1)+2(an﹣1﹣2an﹣2)+…+2n﹣2(a2﹣2a1)+2n﹣1a1=(n+1)•2n﹣1
【点评】此题重点考查数列的递推公式,利用递推公式求数列的特定项,通项公式等,同时考查学生掌握数列的递推式以及等比数列的通项公式的能力.
22.(14分)设椭圆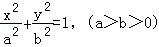 的左右焦点分别为F1,F2,离心率
的左右焦点分别为F1,F2,离心率 ,点F2到右准线为l的距离为
,点F2到右准线为l的距离为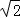
(Ⅰ)求a,b的值;
(Ⅱ)设M,N是l上的两个动点,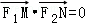 ,
,
证明:当|MN|取最小值时,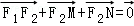 .
.
【考点】K4:椭圆的性质.菁优网版权所有
【专题】14:证明题;15:综合题;16:压轴题.
【分析】(Ⅰ)先根据离心率求得a和c的关系,进而根据F2到右准线为l的距离求得a和c的另一关系式,联立求得a和c,进而根据a,b和c的关系气的b.
(Ⅱ)根据(1)中的椭圆方程求得可知椭圆的焦点坐标,则l的方程可得,设出M,N的坐标,根据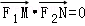 求得得y1y2的值,代入到|MN|的表达式中,根据均值不等式求得|MN|的最小值,根据等号成立的条件求得y1和y2的值,进而求得
求得得y1y2的值,代入到|MN|的表达式中,根据均值不等式求得|MN|的最小值,根据等号成立的条件求得y1和y2的值,进而求得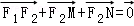 ,证明原式.
,证明原式.
【解答】解:(Ⅰ)因为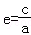 ,F2到l的距离
,F2到l的距离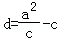 ,所以由题设得
,所以由题设得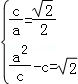 解得
解得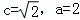
由b2=a2﹣c2=2,得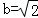
(Ⅱ)由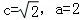 得
得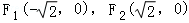 ,l的方程为
,l的方程为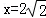
故可设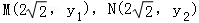
由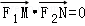 知
知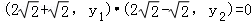
得y1y2=﹣6,所以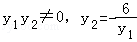
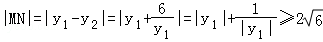
当且仅当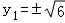 时,上式取等号,此时y2=﹣y1
时,上式取等号,此时y2=﹣y1
所以,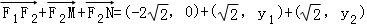 =(0,y1+y2)=
=(0,y1+y2)=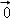
【点评】此题重点考查椭圆基本量间的关系,进而求椭圆待定常数,考查向量与椭圆的综合应用;要熟悉椭圆各基本量间的关系,数形结合,熟练进行向量的坐标运算,设而不求消元的思想在圆锥曲线问题中的应灵活应用.


