2024年全国甲卷理科数学卷高考真题 文字版
(网络收集)2024年全国甲卷理科数学卷高考真题文字版
一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1. 设![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C. 10 D.
C. 10 D. ![]()
2. 集合![]() ,则
,则![]() ( )
( )
A![]()
![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
3. 若实数![]() 满足约束条件
满足约束条件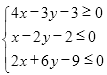 ,则
,则![]() 的最小值为( )
的最小值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
4. 等差数列![]()
![]() 前
前![]() 项和为
项和为![]() ,若
,若![]() ,
,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C. 1 D. 2
C. 1 D. 2
5. 已知双曲线![]() 的上、下焦点分别为
的上、下焦点分别为![]() ,点
,点![]() 在该双曲线上,则该双曲线的离心率为( )
在该双曲线上,则该双曲线的离心率为( )
A. 4 B. 3 C. 2 D. ![]()
6. 设函数![]() ,则曲线
,则曲线![]() 在
在![]() 处的切线与两坐标轴围成的三角形的面积为( )
处的切线与两坐标轴围成的三角形的面积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
7. 函数![]() 在区间
在区间![]() 的大致图像为( )
的大致图像为( )
A. 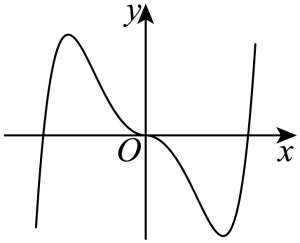 B.
B. 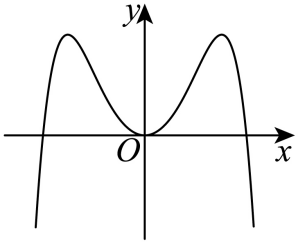
C. 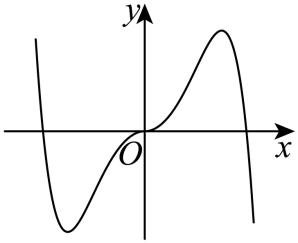 D.
D. 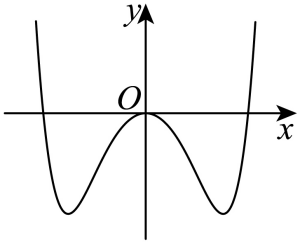
8. 已知![]() ,则
,则![]() ( )
( )
A![]()
![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
9. 已知向量![]() ,则( )
,则( )
A. “![]() ”是“
”是“![]() ”的必要条件 B. “
”的必要条件 B. “![]() ”是“
”是“![]() ”的必要条件
”的必要条件
C. “![]() ”是“
”是“![]() ”的充分条件 D. “
”的充分条件 D. “![]() ”是“
”是“![]() ”的充分条件
”的充分条件
10. 设![]() 是两个平面,
是两个平面,![]() 是两条直线,且
是两条直线,且![]() .下列四个命题:
.下列四个命题:
①若![]() ,则
,则![]() 或
或![]() ②若
②若![]() ,则
,则![]()
③若![]() ,且
,且![]() ,则
,则![]() ④若
④若![]() 与
与![]() 和
和![]() 所成的角相等,则
所成的角相等,则![]()
其中所有真命题的编号是( )
A. ①③ B. ②④ C. ①②③ D. ①③④
11. 在![]() 中内角
中内角![]() 所对边分别为
所对边分别为![]() ,若
,若![]() ,
,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
12. 已知b是![]() 的等差中项,直线
的等差中项,直线![]() 与圆
与圆![]() 交于
交于![]() 两点,则
两点,则![]() 的最小值为( )
的最小值为( )
A. 2 B. 3 C. 4 D. ![]()
二、填空题:本题共4小题,每小题5分,共20分.
13. 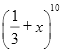 的展开式中,各项系数的最大值是______.
的展开式中,各项系数的最大值是______.
14. 已知甲、乙两个圆台上、下底面的半径均为![]() 和
和![]() ,母线长分别为
,母线长分别为![]() 和
和![]() ,则两个圆台的体积之比
,则两个圆台的体积之比![]() ______.
______.
15. 已知![]() ,
,![]() ,则
,则![]() ______.
______.
16. 有6个相同的球,分别标有数字1、2、3、4、5、6,从中不放回地随机抽取3次,每次取1个球.记![]() 为前两次取出的球上数字的平均值,
为前两次取出的球上数字的平均值,![]() 为取出的三个球上数字的平均值,则
为取出的三个球上数字的平均值,则![]() 与
与![]() 差的绝对值不超过
差的绝对值不超过![]() 的概率是______.
的概率是______.
三、解答题:共70分.解答应写出文字说明,证明过程或演算步骤.第17题~第21题为必考题,每个考题考生必须作答.第22、23题为选考题,考生根据要求作答.
(一)必考题:共60分.
17. 某工厂进行生产线智能化升级改造,升级改造后,从该工厂甲、乙两个车间的产品中随机抽取150件进行检验,数据如下:
| 优级品 | 合格品 | 不合格品 | 总计 |
甲车间 | 26 | 24 | 0 | 50 |
乙车间 | 70 | 28 | 2 | 100 |
总计 | 96 | 52 | 2 | 150 |
(1)填写如下列联表:
| 优级品 | 非优级品 |
甲车间 |
|
|
乙车间 |
|
|
能否有![]()
![]() 把握认为甲、乙两车间产品的优级品率存在差异?能否有
把握认为甲、乙两车间产品的优级品率存在差异?能否有![]() 的把握认为甲,乙两车间产品的优级品率存在差异?
的把握认为甲,乙两车间产品的优级品率存在差异?
(2)已知升级改造前该工厂产品的优级品率![]() ,设
,设![]() 为升级改造后抽取的n件产品的优级品率.如果
为升级改造后抽取的n件产品的优级品率.如果![]() ,则认为该工厂产品的优级品率提高了,根据抽取的150件产品的数据,能否认为生产线智能化升级改造后,该工厂产品的优级品率提高了?(
,则认为该工厂产品的优级品率提高了,根据抽取的150件产品的数据,能否认为生产线智能化升级改造后,该工厂产品的优级品率提高了?(![]() )
)
附: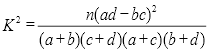
| 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
18. 记![]() 为数列
为数列![]() 的前
的前![]() 项和,且
项和,且![]() .
.
(1)求![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和为
项和为![]() .
.
19. 如图,在以A,B,C,D,E,F为顶点![]() 五面体中,四边形ABCD与四边形ADEF均为等腰梯形,
五面体中,四边形ABCD与四边形ADEF均为等腰梯形,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 的中点.
的中点.
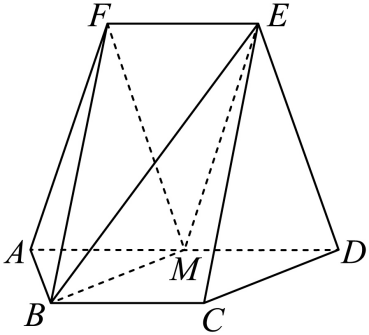
(1)证明:![]() 平面
平面![]() ;
;
(2)求二面角![]() 的正弦值.
的正弦值.
20. 设椭圆![]() 的右焦点为
的右焦点为![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() 轴.
轴.
(1)求![]() 的方程;
的方程;
(2)过点![]() 的直线与
的直线与![]() 交于
交于![]() 两点,
两点,![]() 为线段
为线段![]() 的中点,直线
的中点,直线![]() 交直线
交直线![]() 于点
于点![]() ,证明:
,证明:![]() 轴.
轴.
21. 已知函数![]() .
.
(1)当![]() 时,求
时,求![]() 的极值;
的极值;
(2)当![]() 时,
时,![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
(二)选考题:共10分,请考生在第22、23题中任选一题作答,并用2B铅笔将所选题号涂黑,多涂、错涂、漏涂均不给分,如果多做,则按所做的第一题计分.
[选修4-4:坐标系与参数方程]
22. 在平面直角坐标系![]() 中,以坐标原点
中,以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)写出![]() 的直角坐标方程;
的直角坐标方程;
(2)设直线l:![]() (
(![]() 为参数),若
为参数),若![]() 与l相交于
与l相交于![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
[选修4-5:不等式选讲]
23. 实数![]() 满足
满足![]() .
.
(1)证明:![]() ;
;
(2)证明:![]() .
.


